পাঠ নং-৯ : আইতাক মই কিদৰে পঢ়িবলৈ শিকালোঁ
(ষষ্ঠ শ্ৰেণীৰ পুনৰ আলোচনা)
টোকা: এই পাঠটো যোৱা বছৰ ষষ্ঠ শ্ৰেণীত সম্পূৰ্ণ কৰিব নোৱৰা বাবে ইয়াত থকা গুৰুত্বপূৰ্ণ শব্দসম্ভাৰ আৰু ব্যাকৰণৰ পুনৰালোচনা কৰিবলৈ দিয়া হৈছে।
মৰমৰ ছাত্ৰ-ছাত্ৰীসকল, তোমালোকৰ লগত যদি ষষ্ঠ শ্ৰেণীৰ অংকুৰণ পাঠ্যপুথিখন আছে তেন্তে তাৰ ৯ নং পাঠটো মেলি লৈ এবাৰ পঢ়া আৰু তাত থকা শব্দসম্ভাৰৰ পৰা তলৰ শব্দবোৰৰ অৰ্থ লিখা। অভিধানৰ সহায়তো অৰ্থবোৰ লিখিব পাৰিবা।
কাৰ্য-১: কিতাপত থকা শব্দ সম্ভাৰ বা অভিধানৰ সহায়ত তলত দিয়া শব্দবোৰৰ অৰ্থ লিখা-
| শব্দ | অৰ্থ |
|---|---|
| বয়োজ্যেষ্ঠ | বয়সত ডাঙৰ |
| নিৰক্ষৰ | আখৰ চিনি নোপোৱা |
| অপেক্ষা | বাট চোৱা বা ৰৈ থকা কাৰ্য |
| প্ৰতিবন্ধক | বাধা |
| স্বচ্ছল | ফট্ফটীয়া, স্পষ্ট; সুচল অৱস্থা, চলাচলৰ অসুবিধা নথকা অৱস্থা |
| চৌহদ | চাৰিসীমা |
| সতৰ্ক | সাৱধান |
| অক্ষমতা | অযোগ্যতা |
| দৃঢ় | কঠিন, কঠোৰ |
| ক্লান্তি | ভাগৰ, অৱসাদ |
| স্পৰ্শ | পৰশ; হাতেৰে চুই চোৱা কা্ৰ্য |
| প্ৰাপ্তবয়ষ্ক | পূৰ্ণবয়স্ক, সাবালক |
| অনুপ্ৰেৰণা | উৎসাহ |
| ধাৰাবাহিক | ধাৰাসাৰ, একেৰাহে |
| অতিক্ৰম | পাৰ হৈ যোৱা কাৰ্য |
| উদ্গ্ৰীৱ | ব্যগ্ৰ, উৎকণ্ঠিত |
| উদ্বিগ্ন | উগুল-থুগুল, উৎকণ্ঠিত |
| বাৰম্বাৰ | বাৰে বাৰে |
| ধিক্কাৰ | নিন্দা, তিৰস্কাৰ |
| সংকল্প | প্ৰতিজ্ঞা |
| মণ্ডপ | দেৱালয়, কোনো উৎসৱ বা অনুষ্ঠানৰ বাবে সজা সুসজ্জিত ঘৰ |
| দৰদী | মৰমিয়াল |
কাৰ্য-২ : তোমালোকৰ বিদ্যালয়ত পালন কৰা যিকোনো এটা দিৱস বা উৎসৱৰ বিষয়ে চমুকৈ লিখা।
কাৰ্য-৩ : তলত দিয়া ভাঙনিবোৰৰ যুক্তাক্ষৰ গঠন কৰা। প্ৰতিটো যুক্তাক্ষৰৰে দুটাকৈ শব্দ গঠন কৰা। প্ৰতিটো শব্দৰে একোটাকৈ বাক্য সাজা।
উদাহৰণ:
| ভাঙনি | যুক্তাক্ষৰ | শব্দ | বাক্য |
|---|---|---|---|
| ষ+ঠ= | ষ্ঠ | ষষ্ঠ | মই ষষ্ঠ শ্ৰেণীত পঢ়োঁ৷ |
| জ্যেষ্ঠ | জ্যেষ্ঠ ব্যক্তিসকলক সন্মান কৰিব লাগে৷ | ||
| প+ত= | প্ত | পৰ্যাপ্ত | বায়ুত পৰ্যাপ্ত পৰিমাণৰ অক্সিজেন নাথাকিলে আমি জীয়াই থকাটো অসম্ভৱ৷ |
| সপ্তম | মই সপ্তম শ্ৰেণীত পঢ়োঁ৷ | ||
| স+ক= | স্ক | পুৰস্কাৰ | যোৱা বছৰ ৰচনা প্ৰতিযোগিতাত মই প্ৰথম পুৰস্কাৰ পাইছিলোঁ৷ |
| স্কুল | ক’ভিডৰ বাবে বহু দিনেই আমাৰ স্কুল বন্ধ হৈ আছে৷ | ||
| স+থ= | স্থ | স্থাপত্য | শিৱসাগৰত আহোম যুগৰ স্থাপত্যৰ বহুতো নিদৰ্শন পোৱা যায়৷ |
| স্থিৰ | ছাত্ৰাৱস্থাত আমাৰ মন পঢ়া-শুনাত স্থিৰ কৰিব লাগে৷ | ||
| ন+দ+ৰ= | ন্দ্ৰ | চন্দ্ৰ | চন্দ্ৰ পৃথিৱীৰ একমাত্ৰ উপগ্ৰহ৷ |
| ইন্দ্ৰিয় | আমাৰ দেহত পাঁচটা ইন্দ্ৰিয় থাকে৷ | ||
| দ+ধ= | দ্ধ | বৃদ্ধ | বৃদ্ধ লোকসকলক অৱহেলা কৰা অনুচিত৷ |
| সমৃদ্ধ | অসমখন প্ৰাকৃতিক সৌন্দৰ্যৰে সমৃদ্ধ৷ | ||
| ক+ৰ= | ক্ৰ | ক্ৰমাৎ | ইণ্টাৰনেটৰ ব্যৱহাৰ ক্ৰমাৎ বৃদ্ধি পাই আহিছে৷ |
| ক্ৰয় | বজাৰত বস্তু ক্ৰয়-বিক্ৰয় কৰা হয়৷ | ||
| ন+ধ+উ= | ন্ধু | বন্ধু | বিপদৰ বন্ধুহে প্ৰকৃত বন্ধু৷ |
| সিন্ধু | সিন্ধু সভ্যতা অতি প্ৰাচীন সভ্যতা৷ |
কাৰ্য-৪ : মনত পেলাওঁ আহা-
মই ভাত খালোঁ।
মই ভাত খাই বিদ্যালয়লৈ যাম।
ওপৰৰ বাক্য দুটালৈ মন কৰা৷ প্ৰথম বাক্যটোত ‘খালোঁ’ পদটোৱে বাক্যটোৰ কৰ্তাৰ কাৰ্য সম্পন্ন হোৱা বুজাইছে। তেনেদৰে দ্বিতীয় বাক্যটোত ‘খাই’ পদে কৰ্তাৰ কাৰ্য বা উদ্দেশ্য অসম্পূৰ্ণভাৱে সম্পন্ন কৰা বুজাইছে আৰু ‘যাম’ পদে কৰ্তাৰ উদ্দেশ্য সম্পন্ন কৰা বুজাইছে। এনেদৰে যি পদে বাক্যত কৰ্তাৰ কাম বা কাৰ্য বা উদ্দেশ্য সম্পূৰ্ণ বা অসম্পূৰ্ণভাৱে সম্পন্ন কৰে, সেই পদক ক্ৰিয়া পদ বোলে।
প্ৰথম বাক্যটোৰ ‘খালোঁ’ আৰু দ্বিতীয় বাক্যৰ ‘যাম’ পদে কৰ্তাৰ কাৰ্য সম্পন্ন কৰা বুজাইছে। এনে ধৰণৰ পদবোৰক সমাপিকা ক্ৰিয়া বোলে।
দ্বিতীয় বাক্যটোৰ ‘খাই’ ক্ৰিয়া পদে কৰ্তাৰ কাৰ্য অসম্পূৰ্ণ ৰাখিছে৷ এনে ক্ৰিয়া পদক অসমাপিকা ক্ৰিয়া পদ বোলে।
এতিয়া তলত দিয়া বাক্যবোৰত থকা অসমাপিকা ক্ৰিয়া চিনাক্ত কৰি সেই অসমাপিকা ক্ৰিয়াটো ব্যৱহাৰ কৰি আন এটা বাক্য লিখা।
উদাহৰণ: তাৰ বাবেই মোৰ যোৱাত দেৰি হ’ল।
যোৱাত— দূৰ্বা যোৱাতহে মই আহিলোঁ।
ক) জগত আৰু চহিদুল আহিলে আমি খেলিবলৈ যাম।
উত্তৰ: আহিলে— দেউতা আহিলে দেউতাৰ লগতে মই বজাৰলৈ যাম৷
খ) দেউতাই ভাত খাই গুৱাহাটীলৈ যাব।
উত্তৰ: খাই—ভাত খাই মই স্কুললৈ ওলাম৷
গ) মানসী ঘৰলৈ গ’লে মই যাম।
উত্তৰ: গ’লে— সি খেলিবলৈ গ’লে মই খেলিবলৈ নাযাওঁ৷
ঘ) তুমি চাহ নাখালে ময়ো নাখাওঁ।
উত্তৰ: নাখালে— সময় মতে আহাৰ নাখালে আমাৰ স্বাস্থ্যৰ ক্ষতি হ’ব পাৰে৷
ঙ) তোমালোকে কথা দিলে মই আহিম৷
উত্তৰ: দিলে— অচিনাকি মানুহে বস্তু দিলে মই নাখাওঁ৷
ACTIVITY 1: Look at the picture and complete the sentences:

b) The girl standing alone is holding a styrofoam guitar .
c) Four birds are flying in the sky.
d) The buffalo is looking at the children.
e) There are three animals in the picture, two cows and one buffalo .
f) It is a cloudy (cloudy/ sunny) day.
ACTIVITY 2 (a): Complete the conversation between Neeta and Irfan.


Ans:
Neeta: Hello! My name is Neeta. My hobby is singing. What is your name? What is your hobby?
Irfan: My name is Irfan . My hobby is painting . When do you practice singing?
Neeta: I practice singing every morning . When do you like to paint?
Irfan: I like to paint when I am visiting different places . What types of song do you like singing?
Neeta: I love singing borgeet . What do you like to paint?
Irfan: I like to paint landscapes . I use water colours in my paintings.
Neeta: That’s great! Nice to meet you. Bye!
Irfan: Nice to meet you too. Bye Neeta.
ACTIVITY 2 (b): Now write about yourself.
For example: I am Tulika. I like to dance. I practise dancing in the evening.
I am Rubul .
I like/ love to play flute.
I do at/ in the evening.
ACTIVITY 3: Choose the appropriate words from the box given below and fill in the blanks to
complete the paragraph.
A TRIP TO THE ZOO
One day Ajay and Bijoy planned a trip to the zoo. Ajay packed a bag full of ripe mangoes and a bottle of juice. Ajay carried a bag that had a picture of a beautiful bird on it. First, they went to the ticket counter to buy entry tickets for them. Bijoy went to a nearby shop to buy two packets of biscuits for them. They showed the tickets to the gatekeeper standing at the gate. They entered the zoo. Ajay was excited to see the peacock because he had the picture of a peacock on his bag. They saw lion, crocodile, zebra, ostrich, tiger and snake etc. at the zoo. Ajay was unhappy to see people throwing plastic packets here and there making the place dirty . They sat on a bench and ate the mangoes, biscuits and juice that they carried with them . Bijoy helped Ajay to pack his bag and they returned home.
ACIVITY 4: Choose the correct word and fill in the blanks.
RAJU AND HIS MASK

তোমালোকে ইতিমধ্যে ৬ষ্ঠ শ্ৰেণীত অখণ্ড সংখ্যাৰ বিষয়ে পঢ়ি আহিছা৷
1. অখণ্ড সংখ্যা: শূন্যৰ সৈতে স্বাভাৱিক সংখ্যা আৰু ইহঁতৰ অনুৰূপ বিয়োগাত্মক সংখ্যাবোৰক একেলগে অখণ্ড সংখ্যা বোলে। যেনে: 1, 3, 4, 10, 187, 0, -33, -45, -99, -1006 ইত্যাদি৷
অখণ্ড সংখ্যাৰ কোনো দশমিক বা ভগ্নাংশ নাথাকে৷
কাৰ্য: তলৰ সংখ্যাবোৰৰ পৰা অখণ্ড সংখ্যাবোৰ যুক্তি দৰ্শাই বাছি উলিওৱা৷
987, 9.87, -978, -97.8, \(\frac{22}{7}\), 9\(\frac{12}{17}\), 697, 543
উত্তৰ: 987, -978, 697, 543
2. অখণ্ড সংখ্যাৰ যোগ আৰু বিয়োগৰ বিধি:
(a) যোগ সাপেক্ষে আৱদ্ধ বিধি: দুটা অখণ্ড সংখ্যাৰ যোগফল সদায় এটা অখণ্ড সংখ্যা৷ অৰ্থাও a আৰু b দুটা অখণ্ড সংখ্যা হ'লে a + b ও সদায় এটা অখণ্ড সংখ্যা হ'ব। যেনে:
5 + (-8) = 5-8 = -3
(-9) + (-11) = -9 - 11 = -20
ইয়াত প্ৰথম ক্ষেত্ৰত -3 আৰু দ্বিতীয় য় ক্ষেত্ৰত -20 একোটা অখণ্ড সংখ্যা। ইয়াকে যোগ সাপেক্ষে অখণ্ড সংখ্যাৰ আৱদ্ধ বিধি বোলে।
(b) বিয়োগ সাপেক্ষে আৱদ্ধ বিধি: দুটা অখণ্ড সংখ্যাৰ বিয়োগফল সদায় এটা অখণ্ড সংখ্যা। অৰ্থাৎ a আৰু b দুটা অখণ্ড সংখ্যা হ'লে a - b ও এটা অখণ্ড সংখ্যা হ'ব৷ ইয়াকে বিয়োগ সাপেক্ষে অখণ্ড সংখ্যাৰ আৱদ্ধ বিধি বোলে।
যেনে: 15 - 10 = 5
-4) - (-1) = -4 + 1 = -3
প্ৰতিটো ক্ষেত্ৰত একোটা অখণ্ড সংখ্যা পোৱা গ'ল।
3. অখণ্ড সংখ্যাৰ ক্ৰম বিনিময় বিধি:
(a) যোগ সাপেক্ষে ক্ৰম বিনিময় বিধি: যিকোনো দুটা অখণ্ড সংখ্যা যোগ কৰি পোৱা যোগফলটো সংখ্যা দুটাৰ ক্ৰম সলনি কৰি পোৱা যোগফলৰ সমান৷ অৰ্থাৎ a আৰু b দুটা অখণ্ড সংখ্যাৰ বাবে a+ b = b + a
যেনে: 8 + 10 = 18, 10 + 8=18, গতিকে, 8 + 10 = 10 + 8
(-7) + (-10) = -17,
(-10) + (-7) = -17
গতিকে, (-7) + (-10) = (-10) + (-7)
(b) বিয়োগ সাপেক্ষে ক্ৰম বিনিময় বিধি: বিয়োগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই কিয় ক্ৰম বিনিময় বিধি মানি নচলে চাওঁ আহা। ধৰা হ'ল, a = -64, b = 24
∴ a - b = (- 64) - 24 = - 64 - 24 = -88
আকৌ, b - a = 24 - (-64) = 24 + 64 = 88
∴ a -b ≠ b - a
4. অখণ্ড সংখ্যাৰ সহযোগ বিধি:
(a) যোগ সাপেক্ষে সহযোগ বিধি: যিকোনো তিনিটা অখণ্ড সংখ্যা লওঁ আহা। ধৰা হ'ল, সংখ্যা তিনিটা ক্ৰমে 8, -9 আৰু 15৷
এতিয়া, { 8+ (-9)} + 15 = (৪ - 9) + 15 = - 1+ 15 = 14
আৰু 8+{(-9) + 15} = 8 + (9+15) = 8 + 6 = 14
∴ {8+ (-9)}+ 15 = 8 + {(-9)+15}
অৰ্থাৎ সংখ্যা তিনিটা a, b আৰু c হ'লে
(a+ b) +c= a + (b + c)
সেয়ে অখণ্ড সংখ্যাই যোগ প্ৰক্ৰিয়াত সহযোগ বিধি মানি চলে।
(b) বিয়োগ প্ৰক্ৰিয়াত সহযোগ বিধি: বিয়োগ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাই সহযোগ বিধি মানি নচলে। এটা উদাহৰণেৰে বুজি লওঁ আহা। ওপৰত আলোচনা কৰা সংখ্যাকেইটা লোৱা।
{8-(-9)} - 15 = (৪ + 9) -15 = 17 -15 = 2
8-{(-9)-15} = 8-(-9-15) = 8 + 24 = 32
ইয়াত {8 -(-9)} -15 ≠ 8-{(-9) -15}
অৰ্থাৎ (a-b) - c ≠ a-(b-c)
বা a- (b -c) ≠ (a- b)- c
5. শুদ্ধনে অশুদ্ধ কাষৰ বাকচত লিখা:
1. আটাইতকৈ সৰু স্বাভাৱিক সংখ্যাটো হ'ল 1।
2. আটাইতকৈ সৰু পূৰ্ণ সংখ্যাটো হ'ল 0।
3. শূন্য (0) টো এটা স্বাভাৱিক সংখ্যা।
4. শূন্য (0) টো এটা পূৰ্ণ সংখ্যা।
5. শূন্যটো অখণ্ড সংখ্যা৷
6. তলৰ অখণ্ড সংখ্যাসমূহৰ ক্ষেত্ৰত উপযুক্ত হোৱাকৈ >, = আৰু < চিন ব্যৱহাৰ কৰা।
(a) 0 >. -2
(b) 2+ (-2) <. (-3) + (6)
(c) 4 >. (-7)
(d) (-6) .=. (-5) + (-1)
(e) (-1+ 4) + (17 + 25) >. (-20)
7. তলৰ বাক্যবোৰ শুদ্ধ নে অশুদ্ধ বাকচত লিখা:
(a) যোগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই আৱদ্ধ বিধি মানে।
(b) বিয়োগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই আৱদ্ধ বিধি নামানে।
(c) বিয়োগ প্ৰক্ৰিয়া সাপেক্ষে পূৰ্ণ সংখ্যাই আৱদ্ধ বিধি মানে।
(d) যোগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই ক্ৰমবিনিময় বিধি মানি নচলে।
(e) বিয়োগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই ক্ৰমবিনিময় বিধি মানি চলে।
(f) যোগ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাই সহযোগ বিধি মানি নচলে।
(g) বিয়োগ সাপেক্ষে অখণ্ড সংখ্যাই সহযোগ বিধি মানি নচলে।
(h) তিনিটা অখণ্ড সংখ্যা a, b আৰু c ক্ষেত্ৰত a + (b+c) ≠ (a+b) +c
(i) a-b = b -c
(j) a+ b = b+a
৪. যোগাত্মক অভেদ: তোমালোকে যোগৰ নেওতা শিকোঁতে জানিছিলা যে শূন্য (0) টো যি সংখ্যাৰ লগতে যোগ কৰা নাযাওঁক কিয় যোগফলটো সদায় সংখ্যাটো হয়। যেনে, 1+0 = 1 বা 0+9 =9 = 9 + 0৷ একেদৰে অখণ্ড সংখ্যাৰ ক্ষেত্ৰতো 0 ক অখণ্ড সংখ্যাৰ লগত যোগ কৰিলে যোগফল অখণ্ড সংখ্যাটো পোৱা যায়। যেনে—
25 + 0 = 25 বা 0 +25 = 25
-25 + 0 = -25 বা 0 + (-25) = -25
দেখা গ’ল যে কোনো অখণ্ড সংখ্যাৰ লগত শূন্য (0) ক যোগ কৰিলে বা শূন্য (0) ৰ লগত কোনো অখণ্ড সংখ্যা যোগ কৰিলে সেই অখণ্ড সংখ্যাটোকে পোৱা যায়। সেয়েহে (0) শূন্যক যোগাত্মক অভেদ বুলি কোৱা হয়।
সেয়েহে, এটা অখণ্ড সংখ্যা a ৰ বাবে লিখা হয়—
a + 0 = a = 0 + a
9. শুদ্ধ নে অশুদ্ধ কাষৰ বাকচত লিখা:
(a) (-3) + (-4) এটা পূৰ্ণ সংখ্যা।
(b) (-22 + 15) এটা স্বাভাৱিক সংখ্যা।
(c) 5 + (-5) এটা পূৰ্ণ সংখ্যা।
(d) 5+ 0 = 5 = 0 + 5, যোগাত্মক অভেদৰ ধৰ্ম।
(e) 5 + 0 = 0 + 5, অখণ্ড সংখ্যাৰ ক্ৰম বিনিময় বিধি।
(f) শূন্যক যোগাত্মক অভেদ বুলি কোৱা হয়।
(g) 1 ক যোগাত্মক অভেদ বুলি কোৱা হয়।
(h) -1 আৰু 1 ৰ মাজত কোনো অখণ্ড সংখ্যা নাই।
(i) সংখ্যাৰেখাত 0 ৰ বাঁওফালে থকা সংখ্যাবোৰ হ'ল ঋণাত্মক অখণ্ড সংখ্যা৷
(j) স্বাভাৱিক সংখ্যাবোৰক সংখ্যাৰেখাত স্থাপন কৰিব নোৱাৰি৷
10. যিকোনো অখণ্ড সংখ্যা a ৰ ক্ষেত্ৰত
𝑎 + 0 = 0 + 𝑎 = 𝑎
এই ধৰ্মটোক কোৱা হয় ....
11. x +12 = 4 হ'লে x = -8
12. অখণ্ড সংখ্যাৰ পূৰণ:
(a) পূৰণ প্ৰক্ৰিয়া সাপেক্ষে আৱদ্ধ বিধি: ছাত্ৰ-ছাত্ৰীসকলে পূৰণৰ নেওতা শিকোঁতে দেখিছিলা যে
1 x 3 = 3 (3 এটা অখণ্ড সংখ্যা।)
5 x 6 = 30 (30 এটা অখণ্ড সংখ্যা।)
একেদৰে,
(-3) x 6 = - 18, (18 এটা অখণ্ড সংখ্যা।)
অৰ্থাৎ, a আৰু b যিকোনো দুটা অখণ্ড সংখ্যাৰ ক্ষেত্ৰত (a x b) ও এটা অখণ্ড সংখ্যা।
গতিকে, অখণ্ড সংখ্যাসমূহ পূৰণ প্ৰক্ৰিয়া সাপেক্ষে আৱদ্ধ।
(b) পূৰণ প্ৰক্ৰিয়া সাপেক্ষে ক্ৰম বিনিময় বিধি: তোমালোকে পূৰণৰ নেওতা শিকোঁতে আৰু এটা কথা মন কৰিছিলা যে
6x1=6, আকৌ, 1x6 =6, গতিকে, 6x1=1x6
7 x 3 = 21, আকৌ, 3 x7=21, গতিকে, 7 x 3 = 3x7
(-12) x 6 = -72, আকৌ, 6 x (-12) = -72, গতিকে, (-12) x 6 = 6 x (-12)
গতিকে, যিকোনো দুটা অখণ্ড সংখ্যা a আৰু b ৰ ক্ষেত্ৰত a x b = b x a
অৰ্থাৎ অখণ্ড সংখ্যাই পূৰণ প্ৰক্ৰিয়া সাপেক্ষে ক্ৰম বিনিময় বিধি মানি চলে।
13. অখণ্ড সংখ্যাৰ গুণাত্মক অভেদ: তোমালোকে জানা যে 1 ৰে কোনো সংখ্যাকে পূৰণ কৰিলে পূৰণফলটো সেই সংখ্যাটোৱে হয়। যেনে -
6 x 1= 6
9 x 1= 9
0 x 1= 0
একেদৰে, (-3) x 1 = -3, (-11) x 1 = -11 ইত্যাদি।
যিকোনো অখণ্ড সংখ্যা a ৰ ক্ষেত্ৰত
a x 1 = a =1 x a
অৰ্থাৎ 1 ক অখণ্ড সংখ্যাৰ গুণাত্মক অভেদ বোলে।
14. শুদ্ধ নে অশুদ্ধ কাষৰ বাকচত লিখা:
(a) অখণ্ড সংখ্যাসমূহ পূৰণ প্ৰক্ৰিয়া সাপেক্ষে আৱদ্ধ হয়৷
(b) অখণ্ড সংখ্যাসমূহে পূৰণ সাপেক্ষে ক্ৰম বিনিময় বিধি মানি চলে৷
(c) a x 0= 0 x a = a
(d) 0 x a = 0 = a x 0
15. যিকোনো অখণ্ড সংখ্যা a আৰু b ৰ ক্ষেত্ৰত পূৰণ প্ৰক্ৰিয়া সাপেক্ষে a x b = b x a; এই বিধিটোক কোৱা হয়৷
16. 1ক কোৱা হয় কিয়নো যিকোনো অখণ্ড সংখ্যা a আৰু b ৰ ক্ষেত্ৰতে a x 1 = a আৰু b x 1=b
17. পূৰণ প্ৰক্ৰিয়া সাপেক্ষে অখণ্ড সংখ্যাৰ সহযোগ বিধি: যিকোনো তিনিটা অখণ্ড সংখ্যা, a, b আৰু c ৰ ক্ষেত্ৰত (a x b) x c = a x (b x c) হয়৷ এয়াই হৈছে অখণ্ড সংখ্যাৰ পূৰণৰ ক্ষেত্ৰত সহযোগ বিধি৷ উদাহৰণ স্বৰূপে, তিনিটা অখণ্ড সংখ্যা 5, -6, 8 লৈ চাওঁ আহা৷
{5 x (-6)} x8 = (-30) x 8) = -240
5 x {(-6) x 8} = 5 x(-48) = -240
গতিকে, {5x (-6)} x 8 =5 x {(-6) x 8}
কাৰ্য: তোমালোকে বেলেগ বেলেগ সংখ্যা লৈ পৰীক্ষা কৰি চোৱা -
(a x b) x c = a x (b x c)
18. অখণ্ড সংখ্যাৰ বিতৰণ বিধি:
19. যোগ সাপেক্ষে পূৰণৰ বিতৰণ বিধি: যদি a, b আৰু c তিনিটা অখণ্ড সংখ্যা হয়, তেন্তে
a x ((b+c) = (axb) + (axc)
এয়াই হৈছে অখণ্ড সংখ্যাৰ ক্ষেত্ৰত যোগ সাপেক্ষে পূৰণৰ বিতৰণ বিধি৷
উদাহৰণষ্বৰূপে, 2, -3 আৰু -6 এই অখণ্ড সংখ্যাৰ ক্ষেত্ৰত এই বিধি প্ৰয়োগ কৰি পাওঁ,
2x{(-3)+ (-6)} = 2x(-9) =-18
2x (-3) +2 x (-6) = -6 -12 = -18
গতিকে, 2 x {(-3) + (-6)} = 2x (-3) + 2x(-6)
বিয়োগ সাপেক্ষেও অখণ্ড সংখ্যাই পূৰণৰ বিতৰণ বিধি মানি চলে৷
কাৰ্য: তোমালোকে বেলেগ বেলেগ সংখ্যা লৈ পৰীক্ষা কৰি চোৱা -
a (b + c) = (axb) + (axc)
a x(b-c) = (axb)- (axc)
20. সত্য নে অসত্য কাষৰ বাকচত লিখা:
(a) (3 × 0) × (−9) ≠ 3 × {0 × (−9)} অশুদ্ধ
(b) {6 × (−5)} × 11 = 6 × {(−5) × 11} শুদ্ধ
(c) 10 × {(−5) + (−7)} = {10 × (−5)} + {10 × (−7)} শুদ্ধ
21. পূৰণফল লিখা:
(a) 6x(-10)
(b) (-4)x (-5)
(c) (-12) x0x3
(d) 6x 5x (-8)x (-5)
(e) (-5)x 50x 78
22. বিতৰণ বিধিৰ সহায়ত মান নিৰ্ণয় কৰা। তোমাৰ উত্তৰটো কাষৰ বাকচত লিখিবা।
(a) 5x6 + 5 x(-4)
(b) 6x10 + 11 x 10
(c) 88x99 + 88x1
(d) (-55)x10 + (-55)x90
(e) 999x99 + 99
(f) 58x47 + 94
23. যিকোনো দুটা অখণ্ড সংখ্যাৰ পূৰণফল 51 হ'লে আৰু এটা সংখ্যা (-1) হলে আনটো হ'ব৷
24. অখণ্ড সংখ্যাৰ হৰণ: তোমালোকে দুটা স্বাভাৱিক সংখ্যা বা দুটা পূৰ্ণ সংখ্যাৰ মাজত হৰণ প্ৰক্ৰিয়া শিকি আহিছা। অৱশ্যে পূৰ্ণ সংখ্যাৰ ক্ষেত্ৰত হৰণ কাৰ্যত 0 ৰে হৰণ সম্ভৱ নহয় বুলিও শিকি আহিছা।
অখণ্ড সংখ্যাৰ ক্ষেত্ৰত হৰণ কাৰ্য সমাধা কৰোঁতে আমি এই কথাকেইটা মন কৰিবলগীয়া হয়।
1. এটা ধনাত্মক সংখ্যাক আন এটা ধনাত্মক সংখ্যাৰে হৰণ।
2. এটা ধনাত্মক সংখ্যাক আন এটা ঋণাত্মক সংখ্যাৰে হৰণ।
3. এটা ঋণাত্মক সংখ্যাক আন এটা ধনাত্মক সংখ্যাৰে হৰণ।
4. এটা ঋণাত্মক সংখ্যাক আন এটা ঋণাত্মক সংখ্যাৰে হৰণ।
(a) এটা ধনাত্মক সংখ্যাক এটা ধনাত্মক সংখ্যাৰে হৰণ:
যদি ধনাত্মক সংখ্যা a ক ধনাত্মক অখণ্ড সংখ্যা b ৰে হৰণ কৰা হয় তেন্তে a ÷ b = \(\frac{a}{b}\) = c
য'ত c আন এটা ধনাত্মক সংখ্যা।
যেনে 63 ÷ 9 = \(\frac{63}{9}\) =7
(b) এটা ধনাত্মক সংখ্যাক এটা ঋণাত্মক সংখ্যাৰে হৰণ:
যদি ধনাত্মক অখণ্ড সংখ্যা a ক ঋণাত্মক অখণ্ড সংখ্যা -b ৰে হৰণ কৰা হয়, তেন্তে
𝑎 ÷ (−𝑏)
= \(\frac{a}{-b}\)
= \(\frac{ax(-1)}{-bx(-1)}\)
= \(\frac{-a}{b}\)= c, এটা ঋণাত্মক সংখ্যা
যেনে,
93 ÷ (−3)
= \(\frac{93}{-3}\)
= \(\frac{93x(-1)}{-3x(-1)}\)
= \(\frac{-93}{3}\)
=-31
(c) এটা ঋণাত্মক সংখ্যাক আন এটা ধনাত্মক সংখ্যাৰে হৰণ:
ইয়াত ঋণাত্মক সংখ্যাটো -a আৰু ধনাত্মক সংখ্যাটো b হ'’লে।
(−𝑎) ÷ 𝑏 = \(\frac{-a}{b}\)= c, এটা ঋণাত্মক সংখ্যা৷
যেনে, (-15) ÷ 3 = \(\frac{-15}{3}\)= -5
(d) এটা ঋণাত্মক সংখ্যাক আন এটা ঋণাত্মক সংখ্যাৰে হৰণ:
ধৰোঁ, এটা সংখ্যা -a আৰু আনটো -b৷ এনে ক্ষেত্ৰত
(−𝑎) ÷ (−𝑏)
= \(\frac{-a}{-b}\)
= \(\frac{-ax(-1)}{-bx(-1)}\)
= \(\frac{a}{b}\)= c, এটা ধনাত্মক সংখ্যা৷
যেনে (-90) ÷ (−10)= \(\frac{-9}{-10}\)
=\(\frac{-90x(-1)}{(-1)(-1)}\)
= \(\frac{90}{10}\)
= 9
উদাহৰণ: (i) 510÷ 5 (ii) 625 ÷ (−5) (iii) (-65) ÷ 2
(iv) (-930) ÷ (−2)
সমাধান:
(i) 510÷ 5
= \(\frac{510}{5}\)
=102
(ii) 625 ÷ (−5)
= \(\frac{625}{-5}\)
=-125
(iii) (-65) ÷ 2
= \(\frac{-65}{2}\)
= -32.5
(iv) (-930) ÷ (−2)
= \(\frac{-930}{-2}\)
=\(\frac{930}{2}\)
= 465
25. অখণ্ড সংখ্যাৰ হৰণৰ বিধিসমূহ:
(a) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাৰ আৱদ্ধ বিধি: এটা অখণ্ড সংখ্যাক আন এটা অখণ্ড সংখ্যাৰে হৰণ কৰিলে হৰণফলটো এটা অখণ্ড সংখ্যা নহ'বও পাৰে। যেনে:
15 ÷ 6 = \(\frac{15}{6}\)= \(\frac{5}{2}\), ই অখণ্ড সংখ্যা নহয়।
সেয়ে হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাই আৱদ্ধ বিধি মানি নচলে।
(b) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাৰ ক্ৰমবিনিময় বিধি: অখণ্ড সংখ্যাই হৰণত ক্ৰমবিনিময় বিধি মানি নচলে। যেনে:
(−54) ÷ 9 = −6 কিন্তু 9 ÷ (−54)= \(\frac{9}{-54}\)= \(\frac{-1}{6}\)
দেখা গ'ল যে \(\frac{-1}{6}\) অখণ্ড সংখ্যা নহয়।
গতিকে, 𝑎, 𝑏, 𝑐 অখণ্ড সংখ্যাৰ বাবে 𝑎 ÷ 𝑏 ≠ 𝑏 ÷ 𝑎
(c) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাৰ সহযোগ বিধি: এটা উদাহৰণৰ দ্বাৰা আলোচনা কৰোঁ আহা।
(18 ÷ 6) ÷ 3 = 3 ÷ 3 = 1
আকৌ 18 ÷ (6 ÷ 3) = 18 ÷ 2 = 9
গতিকে দেখা গ'ল (18 ÷ 6) ÷ 3 ≠ 18 ÷ (6 ÷ 3)
সেয়ে হৰণত অখণ্ড সংখ্যাই সহযোগ বিধি মানি নচলে।
অৰ্থাৎ, a,b,c তিনিটা অখণ্ড সংখ্যাৰ বাবে
(𝑎 ÷ 𝑏) ÷ 𝑐 ≠ 𝑎 ÷ (𝑏 ÷ 𝑐)
26. অখণ্ড সংখ্যাক শূন্যৰে হৰণ: এটা উদাহৰণেৰে বুজিবলৈ চেষ্টা কৰোঁ আহা।
উদাহৰণ: 90 ক 0 ৰে হৰণ কৰা।
সমাধান: 90 ÷ 0 = \(\frac{90}{0}\)
এতিয়া আমি এনে এটা সংখ্যা পাম নে যাক 0 ৰে পূৰণ কৰিলে 90 হয় ? নিশ্চয় নাপাম। গতিকে \(\frac{90}{0}\) অৰ্থাৎ 90 ক 0 ৰে হৰণ কৰিব পৰা নাযায়। সেয়ে ই এক অৰ্থহীন কাৰ্য। এতিয়াৰ পৰা তোমালোকে মনত ৰাখিবা যে 0 ৰে কোনো সংখ্যাক হৰণ কৰা সম্ভৱ নহয়।
27. তলৰ প্ৰশ্নবোৰৰ উত্তৰ কাষৰ বাকচত লিখা:
(I)হৰণফল লিখা:
(i) \(\frac{50}{10}\) 5
(ii) \(\frac{-6}{6}\) -1
(iii) 14 ÷ (−5) -2.8
(iv) (−54) ÷ (−6) 6
(v) 0 ÷ (−15) 0
(vi) (−61) ÷ {(−60) ÷ (−1)} -61/60
(vii) {(−72) ÷ (−6)} ÷ (−3) -4
(viii) {(−4) × 18} ÷ 6 kk
(II) (i) যদি 𝑎 ÷ (−7) = 8, তেন্তে, অখণ্ড সংখ্যা a ৰ মান হ'ব -56
(i) যদি 𝑏 ÷ 6 = −5, তেন্তে অখণ্ড সংখ্যা b ৰ মান হ'ব -30
(III) সত্য নে অসত্য কাষৰ বাকচত লিখা:
(i) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাই আৱদ্ধ বিধি মানি চলে।অসত্য
(ii) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাই ক্ৰমবিনিময় বিধি মানি নচলে। সত্য
(iii) হৰণ প্ৰক্ৰিয়াত অখণ্ড সংখ্যাই সহযোগ বিধি মানি চলে। অসত্য
(iv) শূন্যৰে যিকোনো অখণ্ড সংখ্যাকে হৰণ কৰিব নোৱাৰি।সত্য
(v) শূন্যক যিকোনো অখণ্ড সংখ্যাৰে হৰণ কৰিব পাৰি।অসত্য
ৰৈখিক সমমিতি:
তলৰ চিত্ৰবোৰলৈ মন কৰা-

ওপৰৰ চিত্ৰ তিনিটাক একোডাল ফুট চিন থকা সৰলৰেখাই দুটা সমান ভাগত ভাগ কৰিছে।
এইদৰে কোনো চিত্ৰক যদি নিৰ্দিষ্ট ৰেখাৰে দুভাগ কৰিব পৰা যায়, যাতে ভাগ দুটাৰ এটা আনটোৰ দাপোণ প্ৰতিবিম্বৰ সৈতে মিলি যায়, তেন্তে চিত্ৰটোক ৰেখাডাল সাপেক্ষে সমমিত চিত্ৰ বোলা হয়। যিডাল ৰেখা সাপেক্ষে চিত্ৰটো সমমিত হয়,সেই ৰেখাডালক এডাল সমমিতি ৰেখা বা সমমিতি অক্ষ বোলা হয়। আনহাতে চিত্ৰটোৰ এই আকৃতিগত বৈশিষ্ট্যটোক ৰৈখিক সমমিতি বোলা হয়।
তলৰ ত্ৰিভুজ দুটালৈ মন কৰাচোন

|
| সমবাহু ত্ৰিভুজ |

|
| বিষমবাহু ত্ৰিভুজ |
দেখা গ'ল যে, প্ৰথম ত্ৰিভুজটোত ফুট চিহ্নই ত্ৰিভুজটোক দুটা সমান ভাগত ভাগ কৰিছে৷
আনহাতে দ্বিতীয় ত্ৰিভুজটোত ফুট চিহ্নই ত্ৰিভুজটোক দুটা সমান ভাগত ভাগ কৰিব পৰা নাই।
ইয়াৰ পৰা বুজিব পৰা যায় যে প্ৰথম ত্ৰিভুজটো ৰেখা সাপেক্ষে সমমিত আৰু দ্বিতীয় ত্ৰিভুজটো সমমিত চিত্ৰ নহয়।
কাৰ্য-১ : তলৰ চিত্ৰকেইটাৰ পৰা সমমিত চিত্ৰবোৰ চিনাক্ত কৰা আৰু সমমিত চিত্ৰবোৰৰ সমমিত ৰেখা অংকন কৰা-

কাৰ্য-২ : তোমালোকৰ চৌপাশে থকা 5 বিধ সমমিত বস্তু আৰু 5 বিধ সমমিত নোহোৱা বস্তুৰ নাম লিখা৷
উত্তৰ:
| সমমিত হোৱা বস্তু | সমমিত নোহোৱা বস্তু |
|---|---|
| 1. গিলাচ | 1. ঘড়ী |
| 2. কাঁহী | 2. কাঁচি |
| 3. বাটি | 3. চাইকেল |
| 4. বল | 4. বিচনী |
| 5. বাল্টি | 5. ইটা |
কাৰ্য-৩ : তলত দিয়া চিত্ৰবোৰৰ সমমিতি ৰেখাবোৰ ডট্ চিনেৰে চিহ্নিত কৰা-

মন কৰা: এটা সমমিতি চিত্ৰৰ একাধিক সমমিতি ৰেখা থাকিব পাৰে।
কাৰ্য-৪ : তলৰ সমদ্বিবাহু ত্ৰিভুজটোৰ সমমিতি অক্ষডাল চিহ্নিত কৰা

সমমিতি অক্ষ
সমবাহু ত্ৰিভুজ এটাৰ সমমিতি ৰেখা-
ABC সমবাহু ত্ৰিভুজৰ সমমিতি ৰেখা AD, BE আৰু CF৷ অৰ্থাৎ সমবাহু ত্ৰিভুজত সমমিতি ৰেখাৰ
সংখ্যা তিনি।

কাৰ্য-৬: লেখ কাগজত অঁকা কেইটামান জ্যামিতিক আকৃতি তলত দিয়া আছে। চিত্ৰবোৰৰ সমমিতি ৰেখাবোৰ আঁকি দেখুওৱা।
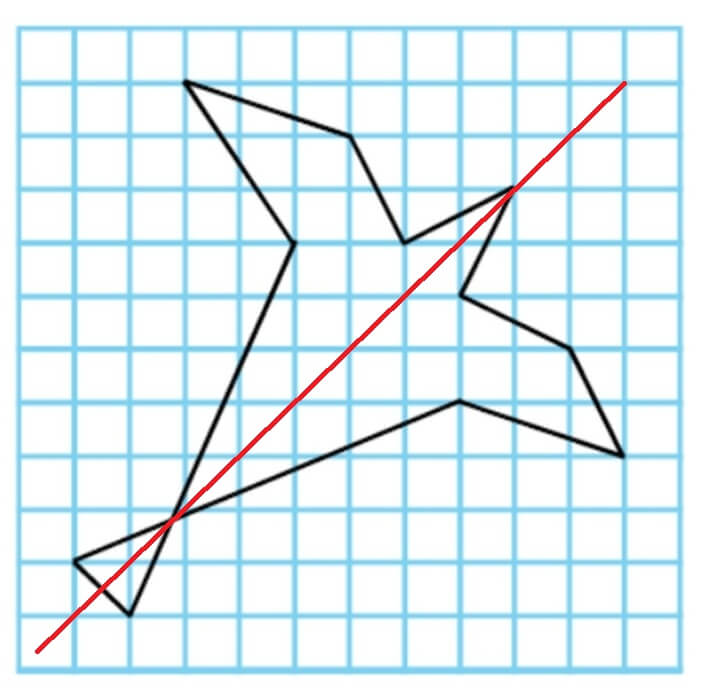
|
| সমমিতি ৰেখাৰ সংখ্যা= |

|
| সমমিতি ৰেখাৰ সংখ্যা= |

|
| সমমিতি ৰেখাৰ সংখ্যা= |
কাৰ্য-৭: বাকচত দিয়া আকৃতিবোৰৰ সমমিতি ৰেখাৰ সংখ্যা নিৰ্ণয় কৰা-
| আকৃতি | সমমিতি ৰেখাৰ সংখ্যা |
|---|---|
| 1. ৰেখাখণ্ড (যিকোনো দৈৰ্ঘ্যৰ) | 1 |
|
2.(a) বিষমবাহু ত্ৰিভুজ
(b) সমদ্বিবাহু ত্ৰিভুজ (c) সমবাহু ত্ৰিভুজ |
0
1
3
|
|
3.(a) বৰ্গ
(b) আয়ত (c) ৰম্বাচ (d) সামন্তৰিক (e) ট্ৰেপেজিয়াম |
4
2
2
0
0
|
| 4. সুষম পঞ্চভুজ | 5 |
| 5. সুষম ষড়ভুজ | 6 |
কাৰ্য-৮ : এটা বৃত্ত অংকন কৰা আৰু ইয়াৰ সমমিতি ৰেখা অংকন কৰা৷ ইয়াৰ সমমিতি ৰেখা কিমান ডাল পালা ? এই সমমিতি ৰেখাডালৰ বৃত্ত সাপেক্ষে কিবা বিশেষ নাম আছে নেকি?
কাৰ্য-৯ : তলত কিছুমান লেখ কাগজত অঁকা চিত্ৰৰ সৈতে একোডালকৈ ৰেখা l1,l2,l3 দিয়া আছে। চিত্ৰবোৰ এনেভাৱে সম্পূৰ্ণ কৰা যাতে সেইবোৰ প্রদত্ত ৰেখা সাপেক্ষে সমমিত হয়৷



কাৰ্য-১০: এখন আয়তাকৃতিৰ কাগজ কাটি দুয়োফালে সম্পূৰ্ণৰূপে মিলাকৈ ভাঁজ কৰা৷ কিমানটা ভাঁজ পালা? প্ৰতিটো ভাঁজৰে একোটা চিত্ৰ অংকন কৰা।
কাৰ্য-১১ : লেখ কাগজত উলম্ব ৰেখা, অনুভূমিক ৰেখা আৰু উভয় ৰেখা সাপেক্ষে সমমিত হোৱাকৈ চিত্ৰবোৰ সম্পূৰ্ণ কৰা।



কাৰ্য-১২ : লেখ কাগজত চিত্ৰ এটা দিয়া আছে। চিত্ৰটোৰ পৰা-

(a) সমমিতি ৰেখাৰ সংখ্যা লিখা৷
উত্তৰ: 2
(b) সমমিতি XY ৰ পৰা EF আৰু 𝐸′𝐹′ ৰ দূৰত্ব কি?
উত্তৰ: 2 একক৷
(c) XY ৰেখাৰ পৰা BC আৰু B'C' ৰ দূৰত্ব জুখি চোৱা, একে পালানে? কিমান পালা?
উত্তৰ: হয়৷ একে পোৱা গ'ল৷ 4 একক পোৱা হ'ল৷
(d) দীঘ নিৰ্ণয় কৰা-
EF = 16 একক
B'C' = 8 একক
DD' = 8 একক
BB' = 8 একক
CC' = 8 একক
কাৰ্য-১৩ : শুদ্ধ উত্তৰটো ৰাখি অশুদ্ধ অংশটো কাটি দিয়া-
a) আমাৰ চৌপাশে দেখি থকা সকলোবোৰ বস্তুৱেই সমমিত হয়/ নহয়।
উত্তৰ: আমাৰ চৌপাশে দেখি থকা সকলোবোৰ বস্তুৱেই সমমিত নহয়।
b) সকলো সমমিত বস্তুৰেই সমমিতি অক্ষ থাকে/ নাথাকে।
উত্তৰ: সকলো সমমিত বস্তুৰেই সমমিতি অক্ষ থাকে।
c) সমমিত বস্তুবোৰৰ সমমিতি অক্ষ এডাল/ দুডাল/ ততোধিক হব পাৰে।
উত্তৰ: সমমিত বস্তুবোৰৰ সমমিতি অক্ষ ততোধিক হব পাৰে।
d) সমমিতি অক্ষ নাথাকিলে বস্তুটো সমমিত হ'ব পাৰে/ নোৱাৰে।
উত্তৰ: সমমিতি অক্ষ নাথাকিলে বস্তুটো সমমিত হ'ব নোৱাৰে।
e) সমমিত বস্তু এটাৰ সমমিতি ৰেখাডালৰ দুয়োফালে থকা অংশ দুটা মিলি যাব/ নাযাব।
উত্তৰ: সমমিত বস্তু এটাৰ সমমিতি ৰেখাডালৰ দুয়োফালে থকা অংশ দুটা মিলি যাব।
f) সমবাহু ত্ৰিভুজ/ সমদ্বিবাহু ত্ৰিভুজ/ বিষমবাহু ত্ৰিভুজৰ সমমিতি ৰেখা নাথাকে।
উত্তৰ: বিষমবাহু ত্ৰিভুজৰ সমমিতি ৰেখা নাথাকে।
মৰমৰ ছাত্ৰ-ছাত্ৰীসকল, তোমালোকে বাৰু আমাৰ চাৰিওফালে ঘটি থকা পৰিৱৰ্তন কিছুমান লক্ষ্য কৰিছানে? যেনে- গুটিৰ পৰা গছ হোৱা, আকৌ গছৰ ফুল ফল হৈ পুনৰ গুটি হোৱা, লোত মামৰে ধৰা, কণমানি কেঁচুৱা এটা ক্ৰমান্বয়ে ডাঙৰ হৈ অহা ইত্যাদি৷ এই পৰিৱৰ্তনসমূহ বুজিবৰ বাবে তলৰ ক্ৰিয়াকলা নিজে কৰি চোৱাচোন। নোৱাৰিলে ডাঙৰৰ সহায় ল'বা।
১৷ এখন কাগজ লোৱা৷ কাগজখন নকটাকৈ ভাঁজ কৰি তোমাৰ ইচ্ছামতে যিকোনো আকৃতিলৈ পৰিৱৰ্তন কৰা, যেনে- নাও, ফুল, ত্ৰিভুজ, টুপী ইত্যাদি৷ এইবাৰ পুনৰ ভাঁজবোৰ খুলি দিয়া৷
কাগজখন পুনৰ আগৰ অৱস্থালৈ আহিলেনে?
উত্তৰ:- হয়৷ কাগজখন পুনৰ আগৰ অৱস্থালৈ ঘূৰি আহিল৷
২৷ এইবাৰ কাগজখন জ্বলাই দিয়া, কাগজখন কিহলৈ পৰিৱৰ্তন হ'ল?
উত্তৰ:- এইবাৰ কাগজখন ছাইলৈ পৰিৱৰ্তন হ'ল৷
এই পদাৰ্থবিধৰ পৰা পুনৰাই কাগজখন পোৱাটো সম্ভৱ হ'লনে?
উত্তৰ:- এই পদাৰ্থবিধৰ পৰা পুনৰাই কাগজখন পোৱাটো সম্ভৱ নহ'ল৷
৩৷ এতিয়া কেইটামান শুকান বুটমাহ লোৱা৷ বুটকেইটা এৰাতি তিয়াই থৈ পাছদিনা এটা পাত্ৰত টুকি ঢাকি ৰাখা, দুদিনৰ মূৰে মূৰে বুটখিনি লক্ষ্য কৰা আৰু পৰিৱৰ্তনসমূহ লিখি ৰাখা৷
প্ৰথম পৰ্যবেক্ষণ (প্ৰথম দিন) -
দ্বিতীয় পৰ্যবেক্ষণ (৩ য় দিন)-
তৃতীয় পৰ্যবেক্ষণ (৫ম দিন)-
তুমি এইখিনিৰ পৰা পুনৰাই শুকান বুট পাব পাৰানে?
উত্তৰ:-
ওপৰৰ এই তিনিটা ক্ৰিয়া পৰ্যবেক্ষণ কৰি কি পাৰ্থক্য দেখিলা চমুকৈ লিখা।
উত্তৰ:-
ওপৰোক্ত ক্ৰিয়া তিনিটাৰ পৰা আমি শিকিলোঁ যে কিছুমান পৰিৱৰ্তন বিপৰীতমুখী অৰ্থাৎ পৰিৱৰ্তন হোৱাৰ পাছতো আগৰ অৱস্থাত ঘূৰাই পাব পাৰি। আনহাতে কিছুমান পৰিৱৰ্তন বিপৰীতমুখী নহয়। অৰ্থাৎ পৰিৱৰ্তন হোৱাৰ পাছত পুনৰ আগৰ অৱস্থাত ঘূৰাই পাব নোৱাৰি।
এতিয়া তোমালোকে তলত দিয়া পৰিৱৰ্তনসমূহ বিপৰীতমুখী হয়নে নহয় চিনাক্ত কৰি লিখা।
| ১) কেঁচা কল এটা পকি যোৱা | নহয় |
| ২) মাটিৰে ৰঙাৱাও, কল, আপেল তৈয়াৰ কৰা | হয় |
| ৩) চাউলৰ পৰা ভাত প্ৰস্তুত কৰা | নহয় |
| ৪) গাখীৰ দৈত পৰিণত কৰা | নহয় |
| ৫) কুঁহিয়াৰৰ পৰা গুৰ প্ৰস্তুত কৰা | নহয় |
| ৬) পানী বৰফ হোৱা | হয় |
| ৭) মম এডাল জ্বলি যোৱা | নহয় |
| ৮) কাঠ-বাঁহৰ পৰা বিভিন্ন সামগ্ৰী তৈয়াৰ কৰা | নহয় |
বিষয়বস্তু: পানীৰ ব্যৱহাৰ
পূৰ্বজ্ঞান:
মৰমৰ ছাত্ৰ-ছাত্ৰীসকল৷ তোমালোকে জানা যে পৃথিৱীৰ পৃষ্ঠভাগৰ প্ৰায় ৭১% পানীয়ে আগুৰি আছে৷ পৃথিৱীৰ এই মুঠ পানীভাগৰ ২.৫%-হে সতেজ পানী আৰু বাকী ৯৮.৮% বৰফ আকাৰে (ডাৱৰত থকা বৰফ বাদ দি) আৰু ভূমিৰ অভ্যন্তৰত জমা হৈ আছে। এই ২.৫% সতেজ
পানীৰ মাত্ৰ ১.২% পানীহে খাবৰ বাবে উপযুক্ত।
জনসংখ্যা বৃদ্ধিৰ লগে লগে মানুহৰ মাজত খোৱাপানীৰ নাটনিয়ে দেখা দিছে৷ ৱৰ্ল্ডোমিটাৰৰ দ্বাৰা বৰ্ণনা কৰা আটাইতকৈ শেহতীয়া ৰাষ্ট্ৰসংঘৰ তথ্য অনুসৰি ২০২১ চনৰ মে' মাহলৈকে বৰ্তমানৰ বিশ্বৰ জনসংখ্যা ৭.৯ বিলিয়ন৷ এজন মানুহক দৈনিক গড়ে 20-40 লিটাৰ পানীৰ প্ৰয়োজন হয়৷ এজন সুস্থ মানুহক দৈনিক খোৱাৰ বাবে গড়ে 2.7 লিটাৰ পানীৰ প্ৰয়োজন হয়৷ সমগ্ৰ বিশ্বত এদিনত খোৱাপানী 5 বিলিয়ন ঘনমিটাৰ প্ৰয়োজন হয়৷ তোমালোকে নিশ্চয় জানা যে
এতিয়াও সকলোৰে বাবে এই বিশুদ্ধ খোৱাপানী যোগান ধৰাটো সম্ভৱ হোৱা নাই৷ অৰ্থাৎ, প্ৰাকৃতিক সম্পদ হিচাপে পানী ব্যৱহাৰৰ ক্ষেত্ৰত আমি সচেতন হৈ পানী সংৰক্ষণ কৰাটো অতি প্ৰয়োজনীয়। আমি পানী ব্যৱহাৰৰ ক্ষেত্ৰত মিত্যব্যয়ী আৰু সজাগ হয়নে? এটা কাৰ্যৰ সহায়ত
আমি কথাষাৰৰ সত্যতা চাওঁ আহা।
ক্ৰিয়া:
তোমালোক প্ৰত্যেকেই তোমালোকৰ নিজ নিজ পৰিয়ালৰ সদস্যসকলে মুঠতে এদিনত বিভিন্ন কামত কিমান পানী খৰচ কৰা সেইটো জানিবৰ বাবে তলৰ তালিকাখন পুৰ কৰাচোন৷
ক্ৰমিক নম্বৰ
কামৰ ধৰণ
এজনৰ বাবে এদিনত সদস্যৰ প্ৰয়োজন হোৱা পানীৰ পৰিমাণ
পৰিয়ালৰ সদস্যৰ মুঠ সংখ্যা
দিনটোত প্ৰয়োজন হোৱা পানীৰ পৰিমাণ (লিটাৰত*) (ঘ)
= (খ) x (গ)
নিৰ্দিষ্ট কামত ব্যৱহাৰ কৰা পানীখিনি পুনৰ বেলেগ কামত ব্যৱহাৰ কৰিব পাৰিনে আৰু কৰানে? (ঙ)
১ মুখ ধোৱা আৰু গা ধোৱা কাৰ্যত
২ খোৱাৰ বাবে
৩ কাপোৰ ধোৱাৰ বাবে
৪ বাচন-বৰ্তন ধোৱাৰ বাবে
৫ ৰন্ধন কাৰ্যৰ বাবে
৬ শস্য, ফুলত দিয়াৰ বাবে
* x (এই চিন দিয়া স্থানত লিখাৰ প্ৰয়োজন নাই।
. * পানীৰ পৰিমাণ জুখিবলৈ তোমালোকে ঘৰত ব্যৱহাৰ কৰা মগ বা গিলাচ ব্যৱহাৰ কৰিব পাৰিবা৷
তোমালোকে তালিকাখনৰ পৰা আমি সাধাৰণতে ব্যৱহাৰ কৰা পানীৰ কিমান অতিৰিক্তভাৱে ব্যৱহাৰ কৰোঁ আৰু কিমান পানীৰ পুনৰ ব্যৱহাৰ কৰিব পাৰি এই কথাখিনি পৰ্যবেক্ষণ কৰি এটি চমুটোকা লিখা। ইয়াৰ বাবে তোমালোকে পাঠটো এবাৰ পঢ়ি চাবা।
তলৰ প্ৰশ্নবোৰৰ উত্তৰ কৰিবলৈ যত্ন কৰাচোন
* পৃথিৱীৰ কিমান শতাংশ খোৱাৰ উপযুক্ত পানী?
উত্তৰ:-
* এজন সুস্থ মানুহক দৈনিক খোৱাৰ বাবে গড়ে কিমান পানী আৱশ্যক হয়?
উত্তৰ:-
* খোৱাৰ বাহিৰে আমি কি কি কামত পানী কমকৈ ব্যৱহাৰ কৰিব পাৰোঁ?
উত্তৰ:-
* চাৰিজনীয়া পৰিয়াল এটিত মাহে নিম্নতম কিমান পানী প্ৰয়োজন হয়?
উত্তৰ:-
* তোমালোকৰ চুবুৰিত মাহে নিম্নতম কিমান পানীৰ প্ৰয়োজন হয়?
উত্তৰ:-
বিষয়: সমাজ বিজ্ঞান
পাঠ নং-১৫ : নতুন ভাৱৰ উত্থান
(ষষ্ঠ শ্ৰেণীৰ পুনৰালোচনা)
ছাত্ৰ-ছাত্ৰীসকল, এই বছৰৰ দৰে যোৱা বছৰটো কভিড-১৯ৰ পৰিপ্ৰেক্ষিতত বিদ্যালয়সমূহ বন্ধ ৰাখিবলগীয়া হৈছিল। যাৰ বাবে নিয়মীয়া পাঠদানৰ বাবে সময় কম হোৱাত আমি কিছুমান
পাঠ অনিচ্ছাকৃতভাৱে বাদ দিবলগীয়া হৈছিল। এই বাদ দিয়া পাঠসমূহ এই বছৰ পুনৰ আলোচনাৰ জৰিয়তে থোৰতে আলোচনা কৰিবলৈ বিচাৰিছোঁ। “নতুন ভাৱৰ উত্থান” নামৰ পাঠটিৰ পৰা জানিবলগীয়া মূল কথাখিনি হ'ল-
* খ্ৰী:পূ: ষষ্ঠ শতিকাত ভাৰতত জৈন ধৰ্মৰ উত্থান হৈছিল।
* জৈন প্ৰবাদমতে ২৪ জন ধৰ্ম প্ৰচাৰকে এই ধৰ্ম প্ৰচাৰ কৰিছিল যদিও ২৪ তম জৈন ধৰ্মৰ প্ৰচাৰত ‘বৰ্দ্ধমান মহাবীৰ'ৰ সময়ত এই ধৰ্মই প্ৰসাৰতা লাভ কৰিছিল। সেয়েহে তেওঁক জৈন ধৰ্মৰ প্ৰৱৰ্তক বুলি জনা যায়।
* বৌদ্ধ ধৰ্মৰ প্ৰৱৰ্তক গৌতম বুদ্ধ কপিলাবস্তু নামৰ এখন ৰাজ্যৰ ৰাজপৰিয়ালত জন্মগ্ৰহণ কৰিছিল। তেওঁৰ ল'ৰালি কালৰ নাম 'সিদ্ধাৰ্থ' আছিল৷
* ২৯ বছৰ বয়সত তেওঁ সংসাৰৰ মায়া-মোহ ত্যাগ কৰিছিল।
* বোধগয়া নামৰ ঠাইত তেওঁ তপস্যা কৰি দিব্যজ্ঞান লাভ কৰিছিল।
* তেতিয়াৰে পৰা তেওঁ ‘বুদ্ধ’ অৰ্থাৎ ‘পৰম জ্ঞানী’ বুলি জনাজাত হৈছিল আৰু তেওঁ প্ৰচাৰ কৰা ধৰ্ম ‘বৌদ্ধ ধৰ্ম' নামে জনাজাত হয়।
ছাত্ৰ-ছাত্ৰীসকল, তোমালোক প্ৰত্যেকেই “নতুন ভাৱৰ উত্থান” পাঠটি মনোযোগেৰে অধ্যয়ন কৰি তলৰ ক্ৰিয়াকলাপসমূহ কৰিবলৈ যত্ন কৰিবা।
কাৰ্য-১ ভাৰতত ‘বৌদ্ধ ধৰ্ম' আৰু ‘জৈন ধৰ্ম'-ৰ উত্থানৰ অন্তৰালত অৰিহণা যোগোৱা কাৰণসমূহ ব্যাখ্যা কৰা৷
কাৰ্য-২ 'বৌদ্ধ' আৰু ‘জৈন' দুয়োটা ধৰ্মই অহিংসা নীতিৰ ওপৰত প্ৰতিষ্ঠিত৷ ইয়াত ‘অহিংসা'-ৰ দ্বাৰা কি বুজাইছে?
কাৰ্য -৩ বৌদ্ধ আৰু জৈন ধৰ্মৰ উভয়ৰে মাজত থকা সাদৃশ্যসমূহ আৰু বৈসাদৃশ্যসমূহ বাছি উলিওৱা।
কাৰ্য-৪ ষষ্ঠ শ্ৰেণীৰ পাঠ নং-১৬ ৰ ১২৪ পৃষ্ঠাত থকা প্ৰাচীন ভাৰতৰ মানচিত্ৰৰ সহায়ত বুদ্ধদেৱে তেওঁৰ মতবাদসমূহ প্ৰচাৰ কৰা স্থানসমূহ বিচাৰি উলিওৱা। বৰ্তমান এই স্থানসমূহ ভাৰতৰে অন্তৰ্গত নে?
কাৰ্য -৫ শুদ্ধ উত্তৰটো বাছি উলিওৱা-
১/ মহাবীৰে তপস্যাৰ অন্তত লাভ কৰা ‘কৈবল্য' ৰ অৰ্থ-
ক) জিতেন্দ্ৰিয় খ) সৰ্বজ্ঞ
গ) আত্মজ্ঞান ঘ) ব্ৰহ্মাৰ্য
২/ গৌতম বুদ্ধৰ জন্ম, বুদ্ধত্ব প্ৰাপ্তি আৰু মহাপৰিনিৰ্বাণ ঘটিছিল-
ক) মাঘ মাহৰ পূৰ্ণিমাত খ) ব'হাগ মাহৰ পূৰ্ণিমাত
গ) আঘোণৰ পূৰ্ণিমাত ঘ) কাতি মাহৰ পূৰ্ণিমাত
৩/ তলৰ কোনটো অসমৰ জনগোষ্ঠীয়ে আজিও বৌদ্ধ ধৰ্মৰ উপাসনা কৰে-
ক) আহোম খ) মিচিং
গ) তিৱা ঘ) খামতি
৪/ বুদ্ধদেৱে তেওঁৰ মতবাদসমূহ প্ৰথমে প্ৰচাৰ কৰিছিল-
ক) বোধগয়াত খ) সাৰনাথত
গ) কপিলাবস্তুত ঘ) তক্ষশীলাত
কাৰ্য-৬
চমুটোকা লিখা-
ক) অষ্টাংগিক মাৰ্গ
খ) ত্ৰিপিটক
গ) বৌদ্ধ বিহাৰ
ঘ) পূৰ্ব


